Andres Andra

Tallinna Nõmme Gümnaasium

Füüsika konspekt. 10 klass, Loodus-, Loodus-korvpall ja Humanitaarsuund.

Tallinna Nõmme Gümnaasium

Füüsika kursuse kava:

1. Füüsika Meetod. Kinemaatika (35 tundi)

2. Dünaamika (35 tundi)

3. Füüsika ja tehnika – Jäävuse seadused ja staaatika elemendid (35 tundi)

1. ja 2. kursus on suundade Humanitaarmeedia ja Loodus (korvpalliharu) õpilastele. Kõik kolm kursust on Loodussuuna õpilastele.

2. Füüsika. Teadusmeetod. Mõõtmine (10 tundi).

Põhimõisted: teadusmeetod, loodusseadus, mikro-, makro- ja megamaailm, füüsika, mõõtmine, mõõtühikute süsteem, mõõtemääramatus, mõõtesuurus, mõõdetava suuruse väärtus, mõõtetulemus, mõõtevahendid, taatlemine

Kinemaatika, liikumise kirjeldamine, Vektorid (20 tundi)

Põhimõisted: kulgliikumine, punktmass, taustsüsteem, kinemaatika, skalaarne ja vektoriaalne suurus, teepikkus, nihe, kiirus, hetkkiirus, kiirendus, vaba langemine, heitkeha.

Ringliikumine (5 tundi)

Põhimõisted: pöördenurk, nurkkiirus, joonkiirus, kesktõmbekiirendus

3. Dünaamika (35 tundi)

Teemad:

Keha impulss ja impulsi jäävuse seadus, reaktiivliikumine, keha kaal

Newtoni seadused. Newtoni esimene seadus, inertsiaalne taustsüsteem. Mass. Jõud. Newtoni teine seadus, jõudude liitmine. Jõu mõõtühik. Newtoni 3. seadus (Galilei relatiivsusprintsiip). Kiirendusega liikuva keha kaal. Kaalutus ja ülekoormus.

Keha energia (energia mõiste süvendatult – kursusel nr. 3. „Staatika elemendid. Jäävusseadused“).

Mehaaniline töö, võimsus, energia. Potentsiaalne ja kineetiline energia. Energia jäävuse seadus mehaanilistes protsessides.

Ühtlaselt kiirenevalt liikuva keha koordinaadi, kiiruse ja kiirenduse määramine uurides kuulikese veeremist rennis.

Ühtlaselt kiirenevalt liikuva keha koordinaadi, kiiruse ja kiirenduse määramine uurides kuulikese veeremist kasutades fotoväravaid.

Jõud looduses

Elastsusjõud. Hookei`i seadus. Gravitatsioonijõud ja gravitatsiooni seadus. Hõõrdejõud ja hõõrdetegur. Keha liikumine raskusjõu mõjul, - elastsusjõu mõjul.

Võnkumine ja lained

Võnkumisega seotud põhimõisted, matemaatiline pendel ja vedrupendel. Matemaatiline pendel, energia muutumine võnkumisel. Võnkumise levimine elastses keskkonnas. Laine levimise kiiruse seos lainepikkuse ja sagedusega. Lainete interferents, Hygensi printsiip, lainete peegeldumine ja lainete difraktsioon.

4. Füüsika ja tehnika – Jäävuse seadused ja staatika elemendid (35 tundi)

Staatika elemendid

Raskuskese. Keha tasakaal pöörlemistelje puudumisel. Pöörlemisteljega kehade tasakaal. Jõu õlg. Jõumoment. Momentide reegel. Keha tasakaalu üldtingimus. Tasakaalu liigid.

Jäävusseadused mehaanikas

Impulss kui vektor. Liikumishulk ja jõuimpulss. Impulsi jäävuse seadus, selle rakendusi. Reaktiivliikumine. Keha mehaaniline olek, oleku muutumine. Mehaanilise töö üldine definitsioon. Töö geomeetriline tõlgendus. Mehaaniline energia ja  võimsus. Kineetiline energia. Kineetilise energia teoreem. Potentsiaalne energia. Potentsiaalne energia raskusjõu väljas. Elastselt deformeeritud keha ja selle olemus ja käitumine.

                1. Füüsika kui loodusteadus

Füüsika uurib looduse kõige üldisemaid ja põhilisemaid seaduspärasusi. Füüsika kasutab füüsika keele oskussõnu ehk füüsikaliste nähtuste, suuruste ja nende mõõtühikute nimetusi. Suuruste tähiste abil kirja pandud füüsikalise sisuga lauseid nimetatakse füüsika valemiteks. Neid kasutatakse füüsikaliste arvutusülesannete lahendamisel. Gümnaasiumi füüsikakursused annavad süsteemse ülevaate kõigest olulisest, mida kaasaegne füüsika looduse kohta antud ajahetkel väita suudab. Formuleeritakse peamised füüsikalised printsiibid ehk tõdemused looduse kohta. Printsiipide paikapidavust tõestab, et loodust vaadeldes veendume ikka ja jälle nende kehtimises. Füüsika õppimisel alustame kokkuvõtliku ülevaatega põhifaktidest, millele tugineb kaasaegne füüsikaline maailmapilt. Kui füüsikaga ei tegeldaks, poleks olemas ka kogu kaasaegset tehnoloogiat ja selle abil loodud hüvesid.

Tartu Ülikooli füüsika instituut

Solvay füüsika konverents 1927.

Kõike seda, mis on väljaspool teadvust ja sellest sõltumatult reaalselt olemas nimetame looduseks ehk materiaalseks maailmaks. Teadvus ei kuulu loodusesse aga inimene kui bioloogiline objekt kuulub sinna. Samuti kuulub sinna kõik inimese loodud ehitised, tehismaterjalid, kosmoseaparaadid, ka saasteained jne. Kõik muu inimtegevusega seotu, nagu poliitika, kunst, religioon, psüühika, sotsiaalsed protsessid jne ei kuulu loodusesse. Füüsika uurib maailmast seda osa mida nimetame looduseks. Füüsikaliseks maailmaks on loodus. Looduses on tasemeline struktueeritus. Igal kindlal struktuuritasemel toimuvaid nähtusi sellel tasemel oluliste seaduspärasuste abil ja see ei sõltu teistele

struktuuritasemetele iseloomulikest nähtustest (planeetide, asteroidide, komeetide jne liikumisel ei ole olulised elektromagnetismi kursuses uuritavad elektrijõud).

 Universumis on väga palju erineva suurusega objekte. Maa on linnuteest umbes kümme astmel 14 korda väiksem.

Järgnevas tabelis on toodud looduse struktuuritasemete skeem, kus vasakul ääres suureneb alt üles uuritava loodusobjekti iseloomulik e. karakteristlik mõõde (pikkus, laius), skeemi keskosas on näited tüüpilisest vaadeldavast objektist. Kolmandas veerus on märgitud vaadeldava struktuuritasemega kõige rohkem tegelev loodusteadus ehk füüsika, geograafia, bioloogia või keemia. Keemia ja bioloogia piirmiste  objektide mõõde 1-100 nm ja on ühesugune. Skeemis saame ka korrata mõõtühikute süsteemi ja eesliiteid.

Loodusteadused annavad kõigile loodusnähtustele teaduslikke kirjeldusi loodusteadusliku meetodi järjekindlal kasutamisel. Esmasel vaatlusel kogutakse andmeid ja seejärel püstitatakse hüpotees. Seejärel korraldatakse hüpoteesi kontrollimiseks eksperiment. Seejärel tehakse andmetöötlus ja lõpuks tehakse järeldus.

Füüsika uurib looduse põhivormide liikumist ja looduses esinevaid vastasmõjusid. Opereeritakse kõigil struktuuritasemetel alates alusosakestest kuni universumi tervikuni. Füüsika nagu kõik loodusteadused, püüavad opereerida arvuliste andmetega. Selleks töötluseks kasutatakse matemaatikat. Füüsika uurib põhivorme (ainet ja välja) täppisteaduslike meetoditega.

Füüsika kasutab kõige rohkem eristudes teistest teadustest, matemaatilisi meetodeid:

Füüsika käsitleb füüsikalisi objekte. Objekt on see ese või nähtus, millega me parajasti tegeleme. Füüsikalisteks objektideks on eelkõige esemed, nimetatakse kehadeks ja kõige üldisemad looduse nähtused (sulamine, aurustumine, tahkestumine, laetud kehade tõmbumine ja tõukumine jne. Kehade vastasmõjusid (tõmbumine, tõukumine) vahendavad väljad on samuti füüsikalised objektid (elektriväli, magnetväli). Objekti kõikide omadustega arvestamine on peaaegu võimatu ja seepärast kasutame lihtsustatud mõttelisi objekte mida nimetame füüsikalisteks mudeliteks.

Füüsika kasutab erilist keelt, milles on kindla tähendusega sõnad ja märgid – füüsikalised suurused, nende mõõtühikud ja suuruste ning mõõtühikute tähised. Füüsikalised suurused  ja mõõtühikud moodustavad süsteemi, milles mõned suurused ja ühikud on valitud põhisuurusteks ja põhiühikuteks. Füüsikaliste suuruste omavahelise seose kohta kehtivaid lauseid, mis on kirja pandud tähiste abil, tunneme me valemitena. Valemite kasutamine võimaldab meil mõtteid lühemalt kirja panna. Füüsikalised suurused ja nende mõõtühikud on samuti looduse mudelid! Mõõtes ühte suurust, näiteks laua pikkust, saame olenemata laua materjalist jne. Looduse ühe lihtsama mudeli füüsikalise suuruse nimega pikkus. Füüsika annab füüsikaliste suurustena kasutada looduse kõige üldisemad mudelid. Näiteks ajaarvestuse aluseks oli Maa ja Kuu perioodiline liikumine. Füüsika seletab päikesesüsteemi komponentide liikumist ja teket kuid ei suuda anda vastust, miks universum tervikuna kiirenevalt paisub. Füüsika tegeleb looduse äärmiste, kõige pisemate struktuuritasemetega.

Füüsika erinevused teistest loodusteadustest on:

1. füüsikal on täppisteaduslike (matemaatiliste) meetodite kõige ulatuslikum rakendamine;

2. füüsika tekitab looduse kõige üldisemad mudelid (füüsikalised suurused ja nende mõõtühikud), kõik teised loodusteadused kasutavad neid;

3. füüsika tegevusala hõlmab kogu loodusobjektide mõõtmete skaalat. Füüsika tegeleb kõige suuremate ja kõige väiksemate loodusobjektidega.

Füüsikaline maailmapilt on kas ühe inimese või kogu inimühiskonna arengu mingile kindlale perioodile iseloomulik ettekujutus maailma (looduse) koostisosadest ja nendevahelistest seostest kui füüsikalistest objektides.

Maailm on keskkond, mis jääb väljapoole inimese minatunnetuse piire

Loodus on inimest ümbritsev ja inimestest sõltumatult eksisteeriv keskkond. Looduses toimuvaid muutusi nimetatakse loodusnähtusteks.

Loodusteadused on koodnimetus kõigile teadustele, mis annavad loodusnähtustele teaduslikke kirjeldusi ja seletusi ning ennustavad loodusnähtusi.

Füüsika on loodusteadus, mis eelistatult täppisteaduslike meetoditega uurib loodust ja tekitab looduse kõige üldisemad mudelid.

Ülesanne:

1. Millised järgmistest objektidest sobivad füüsika mõistes looduse alla: sipelgas, pilv, päkapikk, tellis, arv, neli auto, mõte, teokarp, unenägu?

2. Märkige looduse struktuuritasemete skeemil ära astrofüüsika tööpiirkond. Püüdke märkida ka optika ehk valgusõpetuse, elektriõpetuse, soojusõpetuse ja mehaanika tööpiirkond.

Füüsika, kui loodusteaduse määratlus

Füüsika uurib ja kirjeldab reaalset, olemasolevat loodust. Tegemist on täppisteadusega, kuna uuritava kirjeldamiseks kasutatakse arve ja matemaatika meetodeid. Uuritava looduse kohta saame infot kogemuse teel oma meelte abil ja seda töötleb meie aju! Füüsika on teadus, mis korraga saab oma teadmisi empiirilise ja täppisteadmiste teel!

Inimene on looduse vaatleja, kes saab infot meeleorganite vahendusel ja füüsika on nende vaatluste üldistus. Selleks, et vaatleja saaks loodusest füüsikale vajalikku infot, peavad tal olema:

Meeled (võime saada aistinguid – nägemine, kuulmine, haistmine, maitsmine ja kompimine)

Mälu (võime ifot salvestada ja seda kasutada)

Mõistus (võime loogilisi järeldusi teha)

Kui vaatleja ei saaks aistinguid, poleks tal mingit infot maailmapildi kujundamiseks.

Kui vaatlejal puuduks mälu, siis ei saaks tekkida meelelise tunnetuse keerulisemaid vorme. Mingi osa infost tuleb vältimatult vahepeal salvestada. Mäluta poleks võimalik ka mõtlemine!

Kui vaatlejal puuduks mõistus, ei suudaks ta terviklikke mõttekujundeid liigitada ja omavahel seostada.

Sündmus füüsikas on ükskõik, mis toimub maailmas kindlal ajal ja kindlas kohas

Signaal on sündmust kirjeldava info jõudmine vaatleja närvirakku mingi füüsikalise nähtuse tagajärjel. Signaali moonutavad sündmused on näiteks valguse peegeldus jne.

Füüsika koosneb eri indiviidide tekitatud ja omavahel kooskõlastatud kujutlustest. Kui vaatlejal on piisavalt palju kujutlusi, saab mälu ja mõistust appi võttes moodustada uusi kujutlusi, mida nimetatakse hüpoteesideks. Hüpoteese aga tuleb kontrollida kas vaatleja või teiste antud ala teadlastel.

Loodusteaduslik meetod on jada:

Esmane vaatlus – hüpotees – eksperiment – andmetöötlus – järeldus – hüpoteesi täpsustamine – uus eksperiment – uue teadmise rakendamine jne.

Füüsikaline tunneusprotsess ja kujutlus. Sündmus - helifailist pleieri abil tuleb heli; helisignaal kannab infot; moonutus – lisandub signaali moonutav heli; retseptor – kõrv võtab helid vastu; aisting – närvisignaal suundub kõrvast ajju; taju aju töötleb ja talletab saadud info; kujutlus – aju kujundab sündmusest tervikpildi. Iga vaatleja kujutlused vastavad tema poolt kogetule. Inimeste saavad erinevad aistingud ja ka kuutlused võivad olla erinevad.

Ülesanne kodus:

Kas vaatleja saaks kasutada aja mõistet, kui tal puuduks mälu?

Tooge lisaks tekstis sisalduvale veel üks näide signaali moonutavast sündmusest.

Kas koer või kass on looduse vaatlejad? Kui ei, siis miks?

Kas veebikaameraga ja mikrofoniga varustatud arvuti on vaatleja?

2. Füüsika ja tunnetuspiirid

Nähtavushorisont, sisemine ja väline nähtavushorisont.

Sisemine nähtavushorisont on konkreetse vaatleja teadmiste piir liikumisel piki mõõtmete skaalat üha väiksemate objektide poole.

Väline nähtavushorisont on vaatleja teadmiste piir liikudes mõõtmiste skaalal üha suuremate objektide poole. Füüsika kui teadus määratleb ja nihutab edasi inimkonna kui terviku nähtavushorisonte.

Järgnevates kahes tabelis on toodud mikro-, makro- ja megamaailma horisondid

3. Looduslik meetod füüsikas. Mudelid ja nende piiratus

Vaatleja poolt tunnetuses on jada:

Sündmus, signaal, retseptor, närviprotsess, aisting, taju, kujutlus, mõtteseoste koostamine, uus mõttekujund ehk hüpotees, eksperiment (sihipärane vaatlus), otsustus hüpoteesi tõesuse kohta.

Loodusteaduslik meetod on meetod, mis põhineb vaatluste põhjal hüpoteeside püstitamiseks, nende põhjal ennustuste tegemiseks ja ennustuste paikapidavuse kontrollimiseks katsete (eksperimentide) läbiviimise teel.

Kõik eelnev käsitles eksperimentaalset loodusteadust. Kaasajal teteoreetilist tehakse ka puhtalt teoreetilist teadustööd. Teoreetiline loodusteadus lähtub üldtunnustatud ja kõigis senistes katsetes kinnitust leidnud faktidest looduse kohta. Ta püüab nende faktide alusel loodusnähtuste kirjeldamisel rakendada mingit uut matemaatilist mudelit. Päris uus teooria tugineb mingite seniste mittekasutatud lähte eeldustele ehk postulaatidele Teooria üksikjäreldused tuletatakse antud loodusteaduse üldistest printsiipidest ja arendatava teooria konkreetsetest postulaatidest. Mingit teooriat tunnustatakse lõplikult vaid siis, kui sellest teooriast lähtuvad ennustused on saanud eksperimentaalse kinnituse.

Vaatlus on info kogumine loodusobjekti omaduste kohta objekti mõjutamata, protsessidesse sekkumata.

Hüpotees on katselist kontrollimist vajav teaduslikult põhjendatud oletus.

Katse ehk eksperiment on looduse objekti eesmärgipärane mõjutamine või uuritava loodusnähtuse kunstlik esilekutsumine kontrollitavates tingimustes.

Põhjuslikkus ja juhuslikkus füüsikas

Ülesanne: Milliseid katsetulemusi loetakse piisavalt tõeseks, et neile rajada uusi teooriaid?

4. Mõõtmine, mõõtühikud ja mõõtühikute teisendamine.

Füüsikalise objekti mingi omaduse sellist kirjeldust, mida saab väljendada arvuliselt, nimetatakse füüsikaliseks suuruseks. Tuleb meeles pidada, et füüsikaline suurus on vaid inimese väljamõeldis, vaatlejate ühine kokkulepppeline kujutlus, loodusobjekti mudel. Füüsikaliseks suuruseks on näiteks keha mass, ruumala, liikumise kiirus, temperatuur või aine hulk kehas.

Põhjendatud hinnangu andmist füüsikalise suuruse väärtusele nimetatakse selle suuruse mõõtmiseks. Mõõtmine on füüsikalise suuruse väärtuse võrdlemine mõõtühikuga. Mõõtmine on alati tundmatu suuruse võrdlemine teadaolevaga. Mõõtmine on mingi füüsikalise suuruse konkreetse väärtuse võrdlemine sama suuruse teise, mõõtühikuks võetud väärtusega. Sellise võrdlemise tulemusel saadud arvu nimetame mõõtarvuks ehk mõõdetava suuruse arvväärtuseks.

Mõõtühik on füüsikalise suuruse (nt, pikkus) konkreetne väärtus, mida kokkuleppeliselt kasutatakse sama suuruse teiste väärtuste (nt. pliiatsi pikkus) konkreetne väärtus, mida kokkuleppeliselt kasutatakse sama suuruse teiste väärtuste arvuliseks iseloomustamiseks.

Mõõtmised jagunevad otsesteks ja kaudseteks mõõtmisteks. Otsene on selline mõõtmine, mille korral meid huvitava füüsikalise suuruse saame lugeda mõõteriista skaalalt. Kaudne on mõõtmine, mille korral mõõtetulemus leitakse arvutuste teel. Auto kiirust saab otseselt mõõta spidomeetri abil, aga ka kaudselt, arvutades kiiruse mõõdetud teepikkuse ja sõiduaja jagatisena.

Mõõtmine on mingi füüsikalise suuruse konkreetse väärtuse võrdlemine sama suuruse teise, mõõtühikuks võetud väärtusega. Mõõtmine on võrdlemine mõõtühikuga.

Mõõtühik on füüsikalise suuruse konkreetne väärtus, mida kokkuleppeliselt kasutatakse sama suuruse teiste väärtuste arvuliseks iseloomustamiseks.

Ülesanded:

Miks on loodusteadustes vaja teostada mõõtmisi

Tooge lisaks kiiruse kaudsele mõõtmisele teisi näiteid kaudse mõõtmise kohta.

5. Mõõtühikud

Mõõtühik ja etalon.

Mõõtühik on teadaolev mõõtesuuruse väärtus, millega mõõtmise käigus mõõdetavat suurust võrreldakse. Erinevad mõõtjad peavad kokku leppima ühesugused mõõtühikud. Mõõtühiku kokkuleppimisel kasutatakse näidist, mida nimetatakse etaloniks. Mõõtühiku etalon tuleb kokku leppida nii, et see tugineb looduses väga püsivale objektile. Etaloniks ei sobi näiteks kivi või metallvarras, kuna nende hävimise korral ei saa etaloni täpselt taastada.

Järgnevas tabelis on toodud enamlevinud füüsikaliste ühikute nimetused ja suurused ning suuruste omavaheline suhe.

 Ühikud                                                             Pikkusühik               Aja ühik                                                                           Voolu ühik                                                                       Pinge ühik

Tera T (1000.000.000.000 ehk 10*12)    Tm (10*12 m)                Ts                                                                                           1 TA (10*12A, teraamper)                                            1 TV (10*12V)

Giga G (1000.000.000 ehk 10*9)              Gm (10*9 m)                  Gs                                                                                         1 GA (10*9A, gigaamper)                                               1 GV (10*9V)

Mega M (1.000.000 ehk 10*6)                    Mm (10*6 m)                 Ms                                                                                        1 MA (10*6A, megaamper)                                           1 MV (10*6V)

Kilo K (1000)                                                     Km (10*3 m)                  Ks                                                                                        1 KA (10*3A, kiloampere)                                             1 KV (10*3V)

Ühik (1)                                                                m (meeter)                    s (sekund), 1 minut (1 min)=60 s                            1 A (1 amper)                                                                     1 V (1 Volt)

Detsi d (0,1)                                                       dm (0,1 m)                    1 tund (1h)=60min=3600s                                          1 dA (0,1A)                                                                          1 dV (0,1V)

Senti c (0.01)                                                     cm (10*-2 m)                1päev=24h=1440min=  86400s                                 1 ca (0,01A)                                                                                                1 cV (0,01V)

Milli m (0,001)                                                     mm (10*-3 m)                 ms (10*-3 s, 1 millisekund)                                     1 mA (0,001A)                                                                   1 mV (0,001V)

Mikro μ (0,000001)                                          μm (10*-6 m)                   μs  (10*-6 s, 1 mikrosekund)                                  1 μA (10*-6 A)                                                                    1 μV (10*-6 V)

Nano n (0,000000001)                                   nm (10*-9 m)                   ns (10*-9 s), 1 nanosekund)                                   1 nA (10*-9 A)                                                                   1 nV (10*-9 V)

Piko p (0,000000000001)                              pm (10*-12 m)                 ps (10*-12 s, 1 pikosekund)                                    1 pA (10*-12 A)                                                                  1 pV (10*-12 V)

Takistuse ühik             Juhtivuse ühik              Mahtuvuse ühik          Võimsuse ühik            Jõu ühik                             Töö ühik    Laengu ühik                  

TΩ (10*12 Ω)                      TS (10*12 S)                        TF (10*12 F)                        TW                                          TN                                          TJ                     TC                                           300.000 km/s=300x10*6 m/s

GΩ (10*9 Ω)                        GS (10*9 S)                         GF (10*9 F)                         GW                                         GN                                          GJ                    GC

MΩ (10*6 Ω)                       MS (10*6 S)                         MF (10*6 F)                         MW                                         MN                                         MJ                   MC

KΩ (10*3 Ω)                        KS (10*3 S)                          KF (10*3 F)                          KW                                         KN                                            KJ                  KC

Ω (ohm, oom)                    S (Siemens)                        F ( Farad)                             W (vatt)                                N (newton)                          J (džaul)      C (kulon)

mΩ (10*-3 Ω)                     mS (10*-3 S)                       mF (10*-3 F)                       mW                                        mN                                         mJ                   mC

μΩ (10*-6 Ω)                       μS (10*-6 S)                        μF (10*-6 F)                         μW                                          μN                                          μJ                    μC

nΩ (10*-9 Ω)                          nS (10*-9 S)                           nF (10*-9 F)                            nW                                          nN                                           nJ                    nC                                                                  

Erinevad mõõtühikud ja ühikute süsteemid

Jalg on kokkuleppeline briti meeste keskmine jalalaba pikkus

Toll on pöidlalüli pikkus

Vaks on väljasirutatud pöidla ja väikese sõrme vaheline kaugus

Küünar käsivarre pikkus väljasirutatud sõrmeotsas kuni küünarnukini

Süld laialisirutatud käte sõrmeotste vahe.

Vene tsaaririigis (ka meil) kasutati vene pikkusühikute mõõtude süsteemi

1 toll = 2,54 cm

1 küünar = verssokit = 21 tolli = 53,3 cm

1 arssin = 16 verssokit = 28 tolli = 71,7 cm

1 süld = 3 arssinat =2,13 m

1 verst = 500 sülda = 1,067 km

1 penikoorem = 7 versta = 7,468 km

Briti impeeriumis kasutati SIU süsteemi.

Enamuses riikides kasutatakse SI rahvusvahelist mõõtühikute süsteemi. Alates aastast 1982 on see kohustuslik ka Eestis. 1960 aastal tunnistati see ülemaailmseks.

SI süsteemi põhiühikuteks on:

Meeter m (pikkuseühik), massiühikuks kilogramm kg, ajaühikuks sekund s, temperatuuri ühik kelvin K, elektrivoolu ühikuks amper A, valgustugevuse ükik kandela. 1971 lisati ka ainehulga ühik mool. Väiksemaid ja suuremaid ühikuid saadakse kümmnendeesliitmetega.

Meeter, sekund, kilogramm

Mõõtühikute süsteemid pidevalt arenevad. Meetrit defineeriti kui 1/10000000 Pariisi kohal mõõdetud kaugust ekvaatori ja põhjapooluse vahel. Etaloniks oli Maa.

Nüüd on meter defineeritud teepikkusena,  mille läbib vaakumis valgus 1/299792458 sekundiga.

On valmistatud mitmeid meetri prototüüpe.

Aja põhiühiku sekund algseim etalon oli inimese südametsükli kestvus. Normaalseks loetakse, et inimese süda teeb minutis 60 lööki ja ehk 1 löök on 1 sekund.

Praegu on üks sekund võrdne põhiolekus viibiva tseesium-133 aatomi kõige välimise kihi ainsa elektroni ja aatomi tuuma vastasmõjust tingitud kiirguse 9192631770 perioodiga.

Aatomikell loendab tseesium 133 aatomis toimuvaid võnkeid ja ühe sekundi jooksul toimub 9192631770 võnget.

Massiühik kilogramm (1 kg) on SI süsteemi erandlik mõõtühik, millel puudub looduslik, täpselt taastatav, etalon. Arvatakse, et kilogrammi uus etalon peaks olema puhtast ränist

Praegu on kilogrammi etaloniks nn rahvusvaheline prototüüp plaatina (90%) ja iriidiumi (10%) sulamist silinder mille kõrgus ja läbimõõt on võrdsed (39,17 nm) mida säilitatakse maaaluses hoidlas Pariisi lähedal- saastumise vältimiseks on see kolmekordse klaaskupli all, pääsuvõtmeid hoitakse kolmes eri kohas.

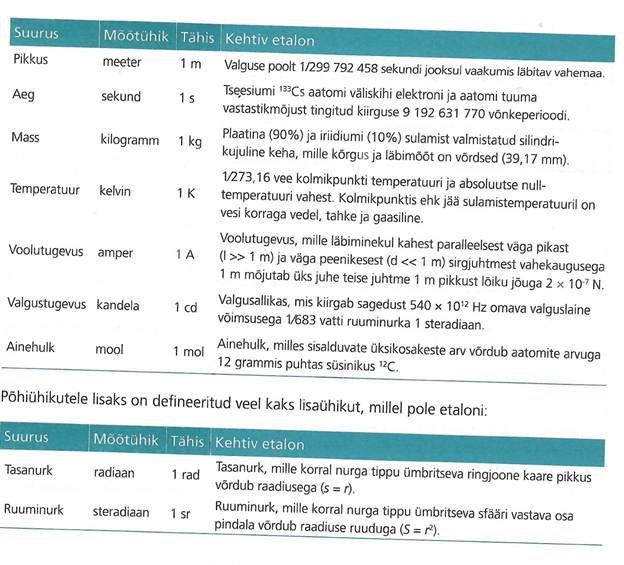
Kasutada tohib korraga vaid ühe ja sama mõõtühikute süsteemi ühikuid. Tabelis on kokku võetud SI seitse põhisuurust ja põhiühikud.

Mõõtesuurus on nähtuse või keha või aine oluline omadus, mida saab teistest omadustest eristada ja arvuliselt kirjeldada.

Mõõtetulemus on mõõtmise teel saadud mõõtesuuruste väärtus

Mõõtesuuruse väärtus on konkreetse suuruse arvuline määrang, mida väljendatakse arvväärtuse ehk mõõtearvu ja mõõtühiku korrutisena.

Etaloniks nimetatakse mõõtühiku kokkuleppimisel kasutatavat näidet.

Küsimus:

Kumb on laiem mõiste, kas mõõtesuurus või füüsikaline suurus?

Mõõtühikute teisendamine.

Rahvusvaheline mõõtühikute süsteem SI on detsimaalne süsteem.

Mõõtühikute endiga võrreldes emamugavalt suurte või väikeste mõõtesuuruste väärtuste väljakirjutamisel kasutatakse kümnendliiteid. Tabelis on toodud suurendavad ja vähendavad eesliited.

SI välised mõõtühikud:

Ühik                                     Tähis

Tund                                     1h= 3600 s

Minut                                   1 min= 60 s

Hektar                                1 ha= 10000 ruutmeetrit

Liiter                                    1 l =0,001 kuupmeetrit

Kilomeetrit tunnis       1 km/h=1/3,6 m/s

Kilovatt-tund                  1kW/h= 3600000 J

Eesliite kasutamine tähendab sellele vastava arvuga korrutamist:

24 km = 24X1000m = 24000 m

Mittesüsteemsetes ühikutes on kõige lihtsam teisendada SI asendades eesliiteed ja ühikud vastavate SI ühikute ja väärtustega:

Näiteks:

72 km/h = 72x1000 m/3600 s= 72000 m/3600 s = 20 m/s

47 kWh = 47x1000 W x 3600 s= 169200000 J = 1,69 x 1000000000J = 169,2 MJ

Isikunimedest tulenevad ühikud on väikeste tähtedeja ja nende mõõtühikute tähised suure tähega. Näiteks kelvin (1K), amper (1A), njuuton (1N), dzaul (1J) ja vatt (1W). Mõõtühikute nimetusi võib esitada ka eesti keelele mugandatud kujul (amper, njuuton, vatt jne.)

Mõõtühikute süsteem on kogum, mille moodustavad kokkulepitus põhiühikud ning neist tuletatud ülejäänud mõõtühikud.

SI põhisuurused on pikkus, aeg, mass, temperatuur, elektrivoolu tugevus, valgustugevus ja aine hulk.

SI põhiühikud on vastavalt meeter (1m), sekund (1s), kilogram (1kg), kelvin (1K), amper (1A), kandela (1cd) ja mool (1mol).

Ülesanded

1. Miks on ajaühiku sekund nimetuseks valitud sõna (Secundus), mis ladina keeles tähendab teine? Mis on siis esimene?

2. Miks säilitatakse kilogrammi rahvusvahelist prototüüpi õhus, aga mitte vaakumis? Hea vaakum võiks ju olla veelgi puhtam kui õhk.

6. Mõõtmise ja täpsus.

Mõõtmise täpsuspiirid ja mõõtemääramatus.

Mõõtmine on mingi füüsikalise suuruse konkreetse väärtuse võrdlemine sama suuruse teise, mõõteühikuks võetud väärtusega!

Mõõtmisel mõjuvad aga alati mingid erinevad välised tegurid! Mõned neist on juhusliku iseloomuga aga on ka süstemaatilised ehk mõõteväärtust kindlas suunas mõjutajad. Kui pall põrkub, ei suuda me prognoosida palli asendit põrkehetkel, seetõttu see asend on mõõteväärtuse juhuslik mõjur. Mõõteviga, mis tekib, kui mõõtka vaatesuund ei ole risti kasutatava skaalaga (nt. Joonlauaga), nimetatakse parallaktiliseks mõõteveaks. Mõõtmise täpsust piirav tegur on mõõtühiku enda pikkus.

Absoluutselt täpne mõõtmine pole põhimõtteliselt võimalik.

Oluline on lisaks mõõteväärtusele hinnata ka mõõtmise täpsust.

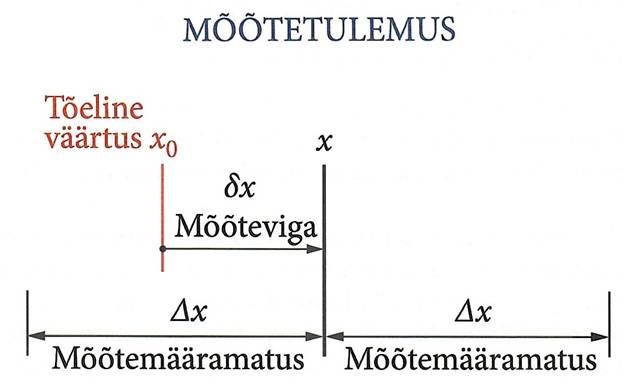
Me peame leppima tõsiasjaga, et mõõtesuuruse tõelist väärtust ei leia me miite kunagi!

Alati seondub mõõtmisega mõõteviga, olgu see kui väike tahes. Mõõteviga on suhteline suurus, mis iga mõõtmisega võib erineda, seondub mõõtmisega mõõtemääramatus.

Tähistame mõõtmise tulemusel saadud mõõteväärtuse tähega x, siis see väärtus erineb kindlasti mõõtesuuruse tõelisest väärtusest x0. Mõõteväärtuse ja suuruse tõelise väärtuse vahet nimetatakse mõõteveaks.

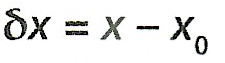
Mida väiksem on mõõteviga, seda täpsem on ka mõõtmine. Mõõteviga on oma olemuslikult juhuslik suurus. Iga järgnev mõõtmine võib eelmisest veidi erineda. Mõõtmisega kaasneb alati teatav teadmatus ehk määramatus. Me same alati mingi tõenäosusega hinnata vahemikku, milles mõõteväärtus asub. Seda mõõtesuuruse väärtuste vahemikku, millesse suuruse tõeline väärtus piisavalt suure tõenäosusega jääb, kirjeldab mõõtemääramatus.

Suuruse x mõõtemääramatus u(x) (inglese keeles uncertainty) on suurus, mis kuulub mõõtetulemuse juurde ja iseloomustab tõenäosuslikult mõõtesuuruse võimalike väärtuste vahemikku. Mõõtemääramatusel on erinevaid tähistusviise. Δx (loe delta x)

Mõõtemmäramatus Δx on mõõtevea δx suurim lubatud väärtus. Mõõtesuurus ei tohi mõõtesuuruse tõelisest väärtusest erineda rohkem kui mõõtemääramatuse Δx võrra. See tähendab, et suuruse tõeline väärtus jääb väärtuste x-Δx ja x+Δx vahele.

Matemaatiliselt väljendab see võrratus

x-Δx<x0<x+Δx

Tõenäosust, et mitte ükski mõõteviga ei ületa konkreetset mõõtemääramatuse väärtust, nimetatakse usaldatavuseks või ka usaldusnivooks.

Kui soovime, et mõõtemääramatusega antav suurima mõõtevea hinnang oleks kindlasti tõene, siis peame kasutama väga suurt Δx väärtust! Mõõtemääramatus esitatakse tavaliselt usaldatavusega  kas 68% või 95%. Eeldades usaldatavust 95%, pannakse mõõtetulemus tavaliselt kirja koos mõõtemääramatusega kujul (x+-Δx) x mõõteühik. Näiteks l=(14,1 +- 0,2) cm või (141+-2) mm. See tähendab, et konkreetse pliiatsi tõeline pikkus jääb 139 mm ja 143 mm vahele tõenäosusega 95%. Kui on tegemist muu usaldatavusega, siis peab selle mõõtetulemus taga eraldi ära märkima.

Iga mõõteriistaga on kaasas täpsust kirjeldav juhis. Alati ei pea mõõtmisi tegema mikromeetriga, tihti piisab väid mõõdulindist.

A- ja B-tüüpi hinnangud mõõtemääramatusele.

Usaldatav mõõtetulemus tuleb alati esitada koos mõõtemääramatusega. Selle hindamiseks on erinevaid meetodeid. Eksisteerib üldjoontes kaks põhilist hinnangu tüüpi, mis on A-tüüpi ja B-tüüpi hinnangud. Neid kutsutakse ka A-tüüpi ja B-tüüpi mõõtemääramatuseks.

Kui me kordusmõõtmisi tehes saame kogu aeg veidi erinevaid tulemusi, siis peame andma mõõtemääramatusele A-tüüpi hinnangu. A-tüüpi mõõtemääramatus on põhjustatud juhuslikest mõjuritest ja see leitakse kordusmõõtmiste tulemustest matemaatilise statistika meetoditega. A-tüüpi määramatust saab vähendada mõõtmiste arvu suurendamisega. Parim hinnang on mõõtetulemuste aritmeetiline keskmine. See saadakse mõõtetulemuste kokkuliitmisel ning selle summa jagamisega mõõtetulemuste arvuga. Mõõtemääramatuse hindamiseks sobib tulemuste hajumist keskväärtuse ümber iseloomustavb statistiline suurus, mis kannab nime standardhälve.

Kui kordusmõõtmised annavad sama tulemuse, siis me ei saa mõõtemääramatust hinnata kordusmõõtmisi tehes. Sellisel juhul anname mõõtemääramatusele B-tüüpi hinnangu ehk tegemist on B-tüüpi määramatusega. B-tüüpi määramatuse hinnang antakse mõõtevahendi tootja poolt, mis kantakse mõõtevahendile või kantakse selle passi. Kui aga sellist infot pole, tuleb mõõtemääramatuseks võtta pool väiksemast skaalajaotusest.

 Voltmeetriga mmõtmisel tuleb anda mõõtemääramatusele B-tüüpi hinnang.

Enamasti esinevad A- ja B-tüüpi määramatus korraga. Liitmääramatus leitakse kui ruutjuur A- ja B-määramatuste ruutude summast. Liitmääramatus on siis:

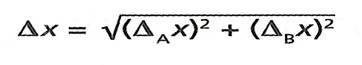
Kokkuvõtvalt:

Mõõtemääramatus on suurus, mis kuulub mõõtetulemuse juurde ja iseloomustab tõenäoslikult mõõtesuuruse võimalike väärtuste vahemikku.

Standardhälve on suurus, mis kirjeldab üksikute mõõteväärtuste juhuslikku hajumist keskväärtuse ümber.

B-tüüpi mõõtemääramatuse hinnangu on teostanud mõõteriista tootja ning mõõtja saab vastava info mõõteriista skaalalt või passist ise statistilesi meetodeid kasutamata

A-tüüpi mõõtemääramatus on põhjustatud juhuslikest mõjuritest ja seda hindab kordusmõõtmiste tulemuste järgi mõõtja statistiliste meetoditega.

Ülesanded

1. Milline on 100m jooksu tulemuse mõõtemääramatus maailmameistrivõistlustel? Kuidas see erineb mõõtemääramatusest kooli kehalise kasvatuse tunnis.

2. Te ostate turul ühe kilogrammi marju. Kui suur oleks mõõtemääramatus selle koguse kaalumisel?

3. Miks absoluutselt täpne mõõtmine pole põhimõtteliselt võimalik?

4. Kas mõõtesuuruste tõeline väärtus eksisteerib looduses või on ainult looduses?

5. Kui suur võiks olla kaugushüppe või kuulitõuke tulemuse mõõtemääramatus kehalise kasvatuse tunnis? Millised tegurid seda põhjustavad?

6. Kui suur võiks olla 100m jooksu tulemuse mõõtemääramatus kehalise kasvatuse tunnis? Millised tegurid seda põhjustavad?

7. Mõõtmised ja mõõteseadus

Mõõtmistel peavad kehtima kindlad kokkulepped, mis tagavad mõõtmise korrastatuse ja väldivad ülearu pikki mõõtmisprotsesside kirjeldusi. Juba keskajal kasutati suuremate linnade ümbruses kohaliku valitsuse poolt kehtestatud mõõtühikuid. Näiteks:

Tallinna vakk (44,277 l), Riia vakk (66,415 l), Tallinna toop (1,09 l), Riia toop (1,32 l). Uusajal tuli aga turgude avardumisel mõõteasjandus ehk metroloogia kogu riigis ühtlustada. Tõsised varalised vaidlused seoses mõõtmistega lahendati kohtutes. Mõõteasjandust õppides tuleb aru saada, et kõik kodanikud peavad hästi mõistma lihtsat tõde, et ebakorrektse mõõtmise alusel esitatud pretensioon on õigustühine.

2004.a. kehtestati Eestis mõõteseadus, mis on avaldatud Riigi Teatajas.

Mõõteseaduses on peamised reguleerimisalad järgmised:

1. Si süsteemi kasutamine on tagatud Eestis

2. SI süsteem on kohustuslik majandustegevuses, rahvatervise ja avaliku ohutuse valdkonnas ja haldus- ning õppetegevuses.

3. Seadus nõuab, et juriidiliselt korrektseid mõõtmisi teostab vastavat tunnistust omav mõõtja, kes kasutab tunnustatud mõõtevahendeid.

4. Mõõtevahendite kontroll ja taatlemine.

5. Mõõtmistegevuse riiklik järelvalve korraldus.

Mõõteseaduses on kirjas kõik olulised mõõteasjanduslikud ehk metroloogilised mõisted ja tegevused.

Mõõtevahendite kontroll ja taatlemine

Mõõtevahend on kindlate omadustega tehniline vahend mõõtmisprotsessi teostamiseks. Mõõtmise puhul on alati tegemist mõõtesignaaliga ehk mõõtearvu kandva infoga. Kõik näidud tuleb vastavusse viia seadusega ehk kalibreerida. Mõõtevahend, mis esitab mõõtesignaali vaatlejale tajutaval kujul, nimetatakse mõõteriistaks. Taatlemine on protseduur, mille käigus taatluslabor kontrollib mõõtevahendi vastavust kontrollitud nõudmistele ja märgib mõõtevahendile vastava taotlusmärgistuse. Taatlusmärgis on taatluskleebis , taatlusplomm või taatlustempli jäljend. See märgis lubab teatud ajavahemiku ehk taatluskehtivusaja jooksul saada usaldatavat mõõtetulemust.

8. Füüsikalised mudelid ja mudelite loomine.

Mudel on loodusobjekti jäljendust, mis asendab originaali selle lihtsamaks mõistmiseks ja uurimiseks. Kõige üldisemaid loodusteaduslikke mudeleid, mida loob füüsika ja mida kasutavad kõik loodusteadused, nimetatakse füüsikalisteks mudeliteks.

Vee molekuli mudelil on ka negatiivne külg, mida kirjeldab eelnev joonis.

Mudeleid liigitatakse ainelisteks ja abstraktseteks. Ainelisi mudeleid kasutatakse siis kui objekt on palja silmaga vaatlemiseks liiga väike või liiga suur.

Tänapäeval kasutataklse ka palju arvutimudeleid ehk animatsioone.

Kui loodusobjekti uuritakse ja kirjeldatakse mitte ainelise mudeli vaid mõtteliste kujutluste ning neid väljendatavate matemaatiliste avaldiste abil, on tegemist abstraktse mudeliga. Vaatleja suudab abstraktseid mudeleid luua mõistuse abil. Näiteks rongi liikumist saab kirjeldada punktmassi mõiste abil. Mõttekujundi abstraktseks mudeliks on matemaatiline avaldis, mis võimaldab objekti kirjeldada mis tahes ajahetkel matemaatilise avaldise kaudu, nt. : x=20 X t

Analüütilise mudeli loomist alustatakse liikumise sihipärase vaatlemisega, millega kaasneb mõõtmine.

Olgu meil näiteks raudteel kilomeetri posti juurde paigutatud ajamõõtja. Ajamõõtjast lähevad signaalid arvutisse. Moodustub andmefail, mis sisaldab kilomeetripostide järjenumbreid ja aejanäitu, mis kulus postini jõudmiseks.

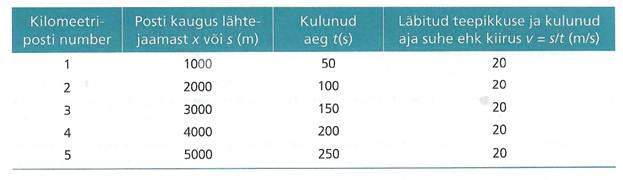
Analüütilise mudeli loomist alustatakse keha liikumise (rongi) sihipärasest vaatlusest, millega kaasneb mõõtmine.

Järgnevaks tegavuseks on andmetöötlus. Selleks koostame graafiku:

Tegemist on võrdelise sõltuvusega ehk lineaarfunktsiooniga y=a X x. Meie mudelis on argumendiks aeg t ja funktsiooniks läbitud teepikkus s=v X t ehk s/t=v. Selline liikumine on ka ühtlane liikumine, milles x on koordinaat ja valemit, mille saime nimetame liikumisvõrrandiks.

Mudeli loomine praktikas

Me teame, et kumminöör venib, kui tõmbame seda ühest otsast ja teine ots on fikseeritud.

Töövahendid: ühest otsast fikseeritud kummipael ja joonlaud. Töö käik: Kinnitame kummipaela ühest otsast ja paigutame vertikaalse joonlaua külge rippuma. Katse tulemused kirjutame tabelisse:

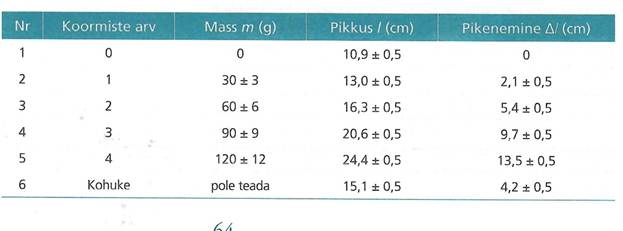
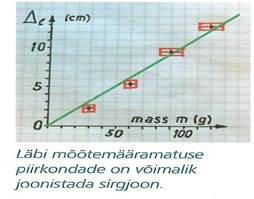
Mõõtmistulemuste analüüs. Tulemusi uurides on näha, et mida suurema massiga on koormis, seda rohkem kummipael pikeneb. Moodustame teljestiku kuhu kanname katsepunktid.

Me ei tohi katsepunkte otsekohe joontega ühendada, see väljendaks veendumust, et oleme absoluutselt täpsed! Me peame iga punkti ümber märkima mõõtemääramatuse piirkonna ehk kasti, mille keskel asub mõõtepunkt, kasti kõrguseks ja laiuseks on vastava mõõtesuuruse kahekordsed mõõtemääramatused. Koostame graafiku, milleks on sirgjoon, mis läbib kõiki mõõtemääramatuse piirkondi:

Seda sirget on võimalik väljendada matemaatilise võrrandi abil. Valime sirgel välja ühe punkti ja leiame graafikult sellele punktile vastava massi ja ja pikenemise. Näiteks m=110 g ja Δl= 11,1 cm. Selle arvupaari abil leiame kui palju venib kumminöör ühikulise massiga koormise mõjul. Jagame pikenemise vastava massiga ja saame:

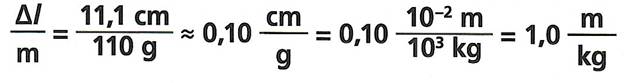
Kasutame seni katses ja analüüsis mõõteühikuna cm ja gr, kuna graafiku koostamisel on neid mugavam kasutada. Lõpptulemus tuleb aga avaldada vastavalt <si süsteemile, kus ühikuteks on meeter  ja kilogramm.

Kui soovime ennustada, kui palju venib kumminöör näiteks 50-grammise koormise korral, tuleb mass saadud arvuga läbi korrutada. Saame:

Δl = 50 g X 0,10 cm/g = 5,0 cm.

Siit saame valemi Δl =0,1 cm/g X m(g).

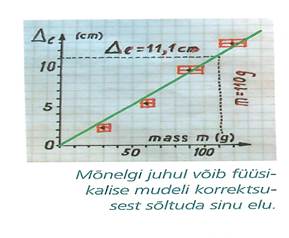
Vaata allpool pilti:

Füüsikaline mudel on alati lihtsustus. Mudel kirjeldab loodust kindlates, fikseeritud tingimustes. Nende puudumisel ei tarvitse mudel anam kehtida!

Mudeli rakendamine. Rakendame eelpoolkirjeldatud mudelit kohukese puhul:

Avadades valemist massi, saame:

Järelikult on uuritava kohukese mass 42 grammi!

Kokkuvõte:

Looduslik mudel on loodusobjekti jäljendus, mis asendab originaali selle lihtsamaks mõistmiseks.

Füüsikaline mudel on kõige üldisem loodusteadlik mudel, mille loob füüsika ja ja mda kasutavad loodusteadused. Rõhutatakse vaid neid omadusi, mis on antud kontekstis olulised.

Füüsikaline mudel kirjeldab loodust kindlates fikseeritud tingimustes, millede puudumisel ei tarvitse see mudel enam kehtida.

Mõõtmine. Nihkkaliiber

Pildil olevat instrumenti nimetatakse nihkkaliibriks. Mõõtetulemuse saab temalt mõõdetava detaili paigutamisel mõõtehaarade vahele. Tulemus loetakse mõõteskaalalt arvestades nihiku skaalal olevaid 10-ndkohti. Selle nihkkaliibril on millimeetrites.

Tavalisel joonlaualt loeme mõõtetulemuse võrreldes objekti joonlaualt ja väikseim ühik

On 1 mm. Järelikult täpsus on 0,5 mm. Konkreetse joonlauaga saab mõõta vahemaad kuni 30 cm.

Praktiline töö „Detaili mõõtmine nihkkaliibri ja joonlaua abil“

1. Mõõta joonlaua ja nihkkaliibri abil detailide (2 detaili) vajalikud mõõdud, et oleks võimalik nende mõõtude abil konstrueerida detaili eskiis-joonis. Mõõdud kanda õpilase poolt konstrueeritud tabelitesse (2 tabelit kokku, üks joonlauaga mõõdetud, teine nihkkaliibriga mõõdetud). Tabelis peavad olema mõõdud, mis võimaldavad nende mõõtude abil konstrueerida detaili eskiisi-joonise. Tabelitesse märkida ka mõõteriistade täpsus.

2. Koostatud tabeli abil joonestada vaba käega detaili eskiis-joonis, millele oleksid kantud ka olulised mõõdud.

3. Eskiis vormistada laboratoorse töö aruandeks millimeeterpaberile. Paberi lehed annab igale õpilase paarile õpetaja.

Kordamisküsimused kontrolltööks

Mis on füüsika valemid

Mis on karakteristlik mõõde

Loodusteaduslik meetod ja selle etapid

Mida uurib füüsika

Mõõdete skaala väiksemast suurema poole

Mis on füüsikalised mudelid

Too mõned näited füüsikaliste põhisuuruste ja põhiühikute kohta

Mis on sündmus

Mis on signaal

Milline on loodusteaduslik meetod, kirjelda

Mis on hüpotees, vaatlus ja katse

Mida nimetatakse mõõtmiseks

Mis on otsene- ja kaudne mõõtmine

Mis on mõõtühik

Too näiteid mõõtühikutest

SI ja teiste mõõtühikute põhierinevus üksteisest

Mis on etalon

Mis on mõõtesuurus (mõõtetulemus)

Nimeta mõned SI välised mõõteühikud

Mis on suurendavad ja vähendavad eesliited (SI), too mõned näited

Mis on mõõtmine ja mõõtetäpsus

Mis on A ja B tüüpi hinnangud

Mehaanika

1. Kinemaatika

Kinemaatika on mehaanika osa, milles kirjeldatakse kehade liikumist ja antakse liikumise analüüsiks meetodid. Kinemaatikas me tegeleme liikumise matemaatilise kirjeldamiseha ja jätame käsitlemata jõud, mis selle liikumise põhjustavad. Et see käsitlus oleks lihtsam, vaatleme ainult punktmassi liikumist. Punktmass on keha mudel, mille korral ei arvestata keha mõõtmeid. Me oletame, et keha mass on koonunud ühte punkti. Me võime ka Maad arvestada punktmassina uurides Maa pöörlemist ümber Päikese. Kui aga uurime Maa pöörlemist oma telje übmer, ei saa me selliselt Maad enam punktmassina käsitleda.

Füüsikanähtused enamasti sõltuvad ajast ja seetõttu annab kinemaatika aluse ka paljude teiste ajas muutuvate suuruste analüüsiks.

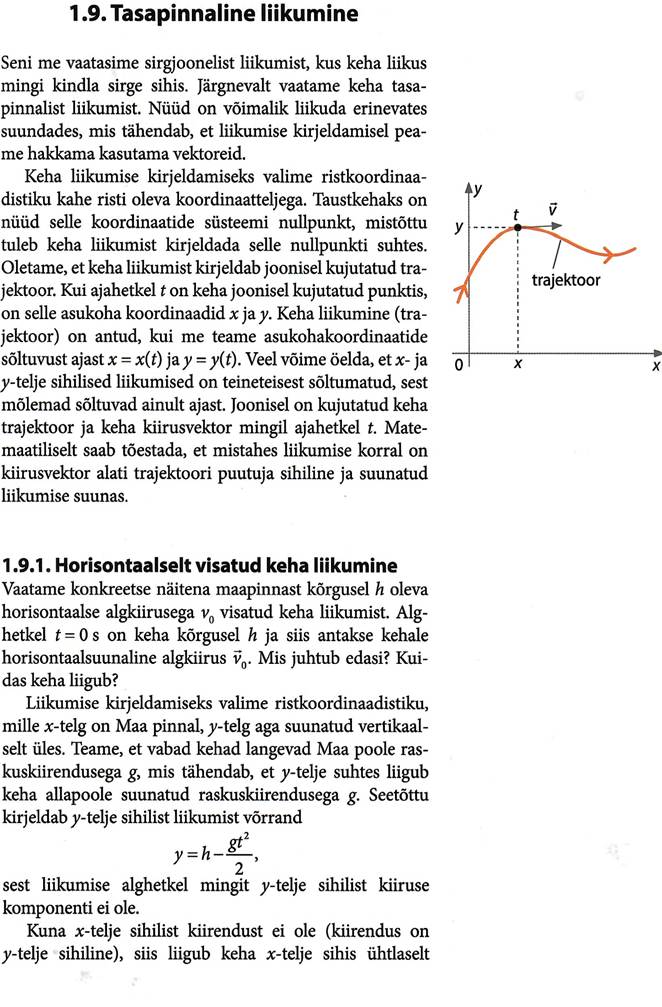
1.1. Liikumine

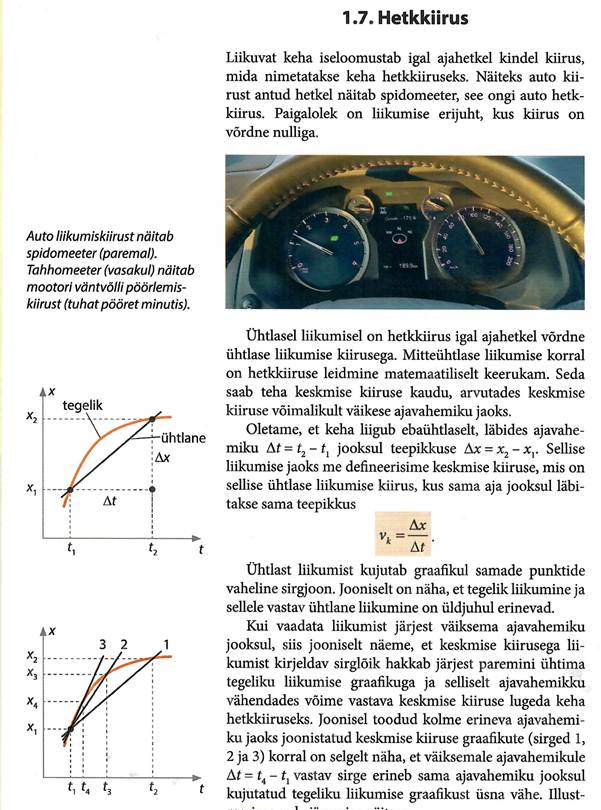
Liikumise mõiste on üheks mehaanika põhimõisteks. Kõik kehad liiguvad ajas ja ruumis. Liikumine on keha asukoha muutumine teiste kehade suhtes nii ajas kui ka ruumis.

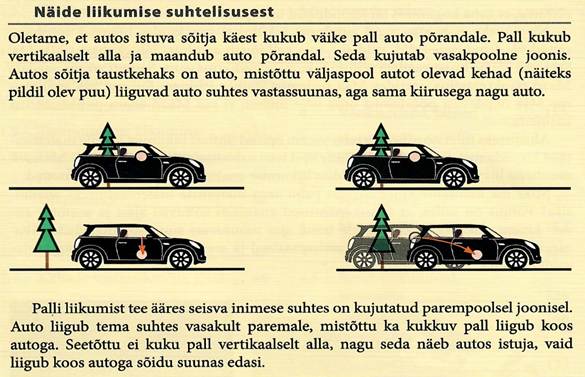
Liiklemise kirjeldamiseks tuleb alati valida mingi kindel taustkeha. Kui näiteks auto läbib ühest kohast teise vahemaa 50 km, siis tee ääres oleva inimese seisukohalt läbisid nii auto kui ka selles olev inimene 50 km. Vaatleme sama situatsiooni autos oleva inimese seisukohalt on ta jõudnud ühest kohast teise sammugi liikumata. Autos olija vaatleb liikumist auto suhtes, auto aga tema suhtes seisab paigal. Kui ruumis liiklemisele võtta lisaks ka aja mõõde ehk mõõta aega, siis ajamõõtjat nimetatakse kellaks. Taustkeha ja kell moodustavad taustsüsteemi. Taustsüsteemiga seotakse mingi koordinaatteljestik. Rääkides edaspidi liikumisest,, eeldame, et meil on valitud mingi kindel taustsüsteem ja vaadeldav liikumine on seotud selle taustsüsteemiga.

Keha liikumine on tema asukoha muutumine ruumis teiste kehade suhtes mingi aja vältel.

Liikumine põhineb mõistetele ruum ja aeg.

Mõisted aeg ja ruum tulenevad inimeste igapäevasest praktikast. Neid ei saa defineerida, kuna puuduvad veelgi üldisemad mõisted, millele need definitsioonid võiksid tugineda. Need on füüsikas kui põhimõisted. Me tajume, et üks ese on teisest kõrgemal, kaugemal, paremal või vasakul jne. See loob meile ruumilise ettekujutuse ümbritsevast maailmast. Aja mõiste on välja kujunenud inimkogemusest korduvate (perioodiliste) nähtuste tajumisel. Aeg ja ruum mõistetena esinevad alati koos. Ruumi ei ole väljaspool aega! Aega ja ruumi saab kirjeldada ainult võrdluse abil. Meie vaatleme mehaanilist liikumist, mis on küllaltki keeruline nähtus.

Vaatleme alul liikumise erinevaid liike:

1.1.1. Sirgjooneline liikumine

Võtame x-telje sirgjoonelise liikumise kirjeldamiseks.

Keha asukoht on määratud koordinaattelje 0-punkti suhtes vastava x-koordinaadiga. Nii on punkti A korral x=3m, st punkt on 0-punktist 3m kaugusel. Punkt B aga x=-2m, mis tähendab, et see on 0-punktist 2m vasakul. Keha liikumisel tema asukoht x-teljel muutub, see aga tähendab, et liikumist kirjeldav x-koordinaat on ajast sõltuv suurus ja seda saab anda mingi ajast sõltuva funktsioonina

                                                                 x = x(t)

Sellist ajast sõltuvust, mis kirjeldab keha liikumist x-teljel nimetame keha liikumisvõrrandiks.

Kommentaarid eelpooltoodule:

1. Taustkehaks on x-telje 0-punkt

2. Erinevalt matemaatikast on x-koordinaat nüüd füüsikaline suurus ja näitab kaugust koordinaatide nullpunktist. Seetõttu on koordinaat kindla ühikuga suurus.

Oluline on, milliseid keha punkte liikumisel vaatleme.

Ainepunkt

Kulgliikumine on selline liikumine, kus keha kõik punktid liiguvad mööda ühesuguseid jooni ehk trajektoore mööda. Näiteks keha vaba langemine, libisemine mööda siledat pinda, vaguni liikumine mööda raudteen jne. Sellist liikumist nimetatakse ka translatoorseks liikumiseks. Sellise liikumise kirjeldamiseks piisab vaid keha ühe punkti liikumise kirjeldamist. Millist keha punkti me liikumise kirjeldamisel eelistame. Eriti oluline on see siis, kuihakkame keha mõju teisele kehale arvestama. Igasugune mõju sõltub kaugusest. Kui me vaatleme keha ennast kui punkti, siis eelistatud küsimus jääb kõrvale.

Anepunktiks nimetatakse füüsikalist keha, mille mõõtmed on palju väiksemad, kui selle keha ja antud tingimustes vaadeldavate teiste kehade vahelised kaugused.

Tavaliselt loetakse, et praktilistes arvutustes, kui kehade vaheline kaugus on üle 10 korra suurem keha enese mõõtmetest, saame sellist keha käsitseda ainepunktina ehk punktmassina. Teatud tingimustes võime ka Maad käsitseda punktmassina, kui taustsüsteemiks on maailmaruum. Füüsikalise keha käsitsemine ainepunktina (punktmassina) lihtsustab liikumise kirjeldamist.

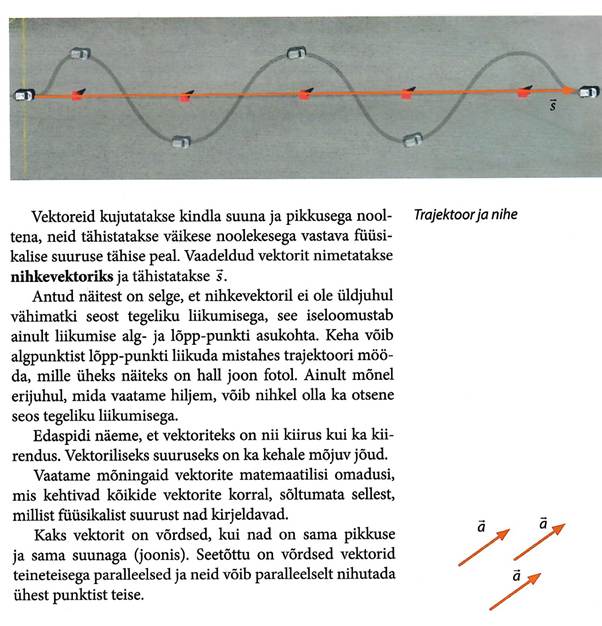
Läbitud tee. Nihe

Keha liikumine on alati seotud tema asukoha muutumisega ruumis mingite teiste kehade suhtes. Kõige olulisem on mõõta vahemaid. Kui keha asus liikumise alul punktis A ja lõpus punktis B, siis neid kahte punkti ühendava sirglõigu pikkus kujutabki endast punktide A ja B vahemaad AB. Üldiselt, mida suurem on vahemaa AB, seda kaugemale on keha liikunud. Selline ettekujutis ei ole aga alati täpne. Näiteks sportlase jooksmisel 400m staadionil, kui ta läbib iga ringiga 400m. Selline liikumine sunnib meid kasutusele võtma kaks erinevat mõistet: keha liikumisel läbitud tee pikkuse ja sooritatud nihke mõiste.

Keha poolt mingi ajavahemiku vältel läbitud trajektoori lõigu pikkust nimetatakse sellel ajavahemikul läbitud tee pikkuseks.

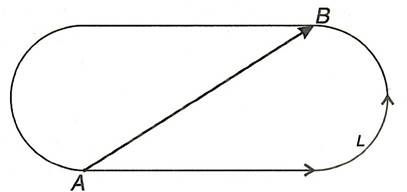
Jooksja liikumisel staadionil punktist A punkti B tee ongi kõvera ALB pikkus. Samal ajal on jooksja nihkunud punktist A punkti B ja siit järeldub, et tema nihke suurust võib mõõta kui vahemaad punktide A ja B vahel (sirglõik AB pikkus). Tema uue asukoha leidmiseks on vaja teada ka sooritatud nihke suunda.

Keha nihkeks liikumisel ühest punktist  teise punkti nimetatakse neid kahte punkti ühendavat sirglõiku.

Jooksja nihke absoluutväärtus on võrdne siin sirglõigu AB pikkusega, see erineb aga märgatavalt läbitud teepikkusest. Sirglõik AB omab kindlat suunda, mis ühtib jooksja liikumise suunaga, kuna on tähtis, kas liigume punktist A punkti B, mitte vastupidi. Nihe on füüsikaline suurus, mis erinevalt läbitud teepikkusest, otstarbekas kujutada  suunatud lõigu ehk vektori abil. Nihkevektori pikkus ehk moodul väljendab nihke arvulist väärtust, tema suund aga nihkumise suunda.

Tuues elust näite taksosõidust, siis veendume, et tasume taksojuhile mitte nihke pikkuse vaid läbitud teepikkuse eest, mis võib olla märksa pikem läbitud nihke pikkusest.

Korvpalli võistluses pallur läbib umbes 5 km, siis on tegemist läbitud tee pikkusega, mitte läbitu nihkega, mis võib olla vaid paar meetrit! Läbitud tee pikkust kui ka nihet mõõdetakse rahvusvahelises mõõtühikute süsteemis SI meetrites. 1 meeter on 1/40 000 000 Pariisi läbiva mediaani pikkusest. 1 meeter on vahemaa, mida valgus läbib vaakumis 1/299792458 sekundiga (valguse kiirus vaakumis on 299792458 m/s).

Järgnevalt vaatleme füüsika ülesandeid mehaanikas, konkreetselt käsitleme mõisteid. Palun vastata koduse ülesandena enda konspekti osa 1.1, 1.4, 1.8, 1.13, 1.19, 1.21.

Ühtlane liikumine

Ühtlane liikumine on liikumise lihtsaim erijuht. Mistahes võrdsetes ajavahemikes läbitakse võrdsed teepikkused. Siin on teepikkuse s ja aja t suhe jääv suurus, mida nimetatakse ühtlase liikumise kiiruseks.

V=s/t

Ühtlane liikumine on seega jääva kiirusega liikumine, liikumise käigus kiirus ei muutu.

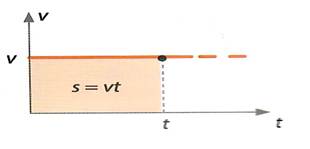
Kiiruse graafikuks on horisontaalne sirgjoon.

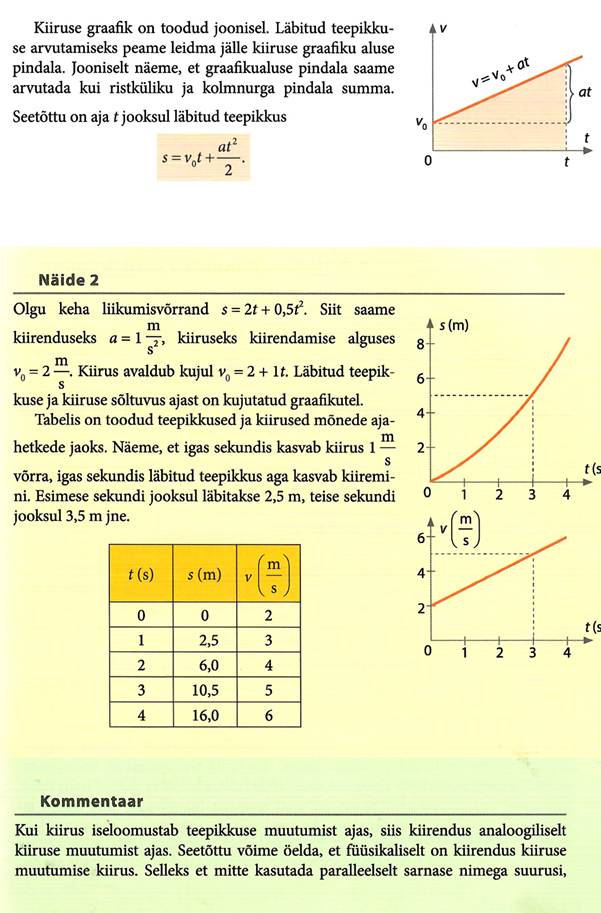
Läbitud teepikkuse arvutamine

Teades kiirust v, saame ühtlasel liikumisel aja t jooksul arvutada läbitud teepikkuse,

S=vt

Ühtlase liikumise korral on teepikkuse ajast sõltuvuse graafikuks sirgjoon. Teades teepikkuse graafikut, saame arvutada kiiruse

v=s/t

Kui jälgime nüüd  kiiruse graafikut, näeme, et läbitud teepikkus on võrdne kiiruse ja aja korrutisega ehk läbitud teepikkus on arvuliselt võrdne kiiruse graafiku alla jääva pindalaga, joonisel seega ristküliku pindalaga. Seos kiiruse graafiku alla jääva pindala ja läbitud teepikkuse vahel on üldine.

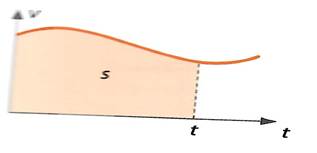
Kui liikumine on mitteühtlane, siis kiirus liikumisel muutub ja kiiruse graafik ei ole sirgjooneline, läbitud teepikkus on ikka võrdne graafiku alla jääva pindalaga.

Ühikud

Füüsikalised suurused on kindla ühikuga suurused. Nii on seda liikumise kirjeldamisel x koordinaat, mis peab olema antud kindla pikkusühikuga. Enamasti on pikkusühikuks meeter (1m) ja ajaühikuks sekund (1s). Sellisel juhul saame kiiruse ühikuks 1 m/s (üks meeter sekundis). Tavaelus kasutame kiiruse ühikut 1 km/h (üks kilomeeter tunnis). Neid ühikuid saab omavahel teisendada, teades, et 1 km=1000m ja 1 h=3600 s. Näiteks 90km/h=25m/s.

Ühtlane sirgliikumine

Sirgliikumise kirjeldamiseks valime x-telje. X-teljel saab liikuda kahes erinevas suunas (nii positiivses, kui ka negatiivses), saame

Kiiruse ees olev märk määrab ära liikumise suuna. Kui kiiruse ees on plussmärk

X=vt,

siis keha liigub positiivses suunas viirusega v, kui aga

x=-vt,

siis liigub sama kiirusega v, aga x-telje negatiivses suunas.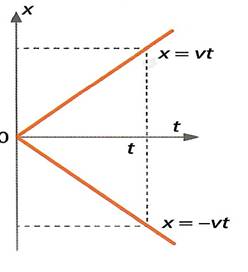

Kiirus on alati positiivne suurus ja iseloomustab ajaühikus läbitud teepikkust. Vale on öelda, et x=-vt on kiirus negatiivne. Miinusmärk kiiruse ees näitab liikumise suunda, keha liigub x-telje negatiivses suunas.

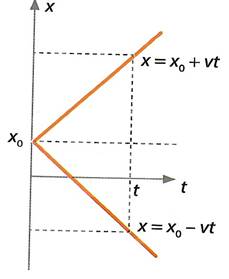
Kui me eeldasime, et ajahetkel t=0s hakkab keha liikuma keha koordinaatide alguspunktist x=o m. Seda on võimalik üldistada juhule kui keha hakkab liikuma alghetkel t=0 s hakkab keha liikuma mingist x telje punktist X0. Sellel juhul kirjeldab ühtlast sirgliikumist võrrand:

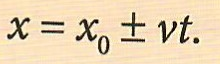
Vahe on vaid selles, et ajahetkel t=0 shakkab keha liikuma punktist X0 ja sõltuvalt kiiruse ees olevast märgist liigub seal ka x-telje positiivses või negatiivses suunas.

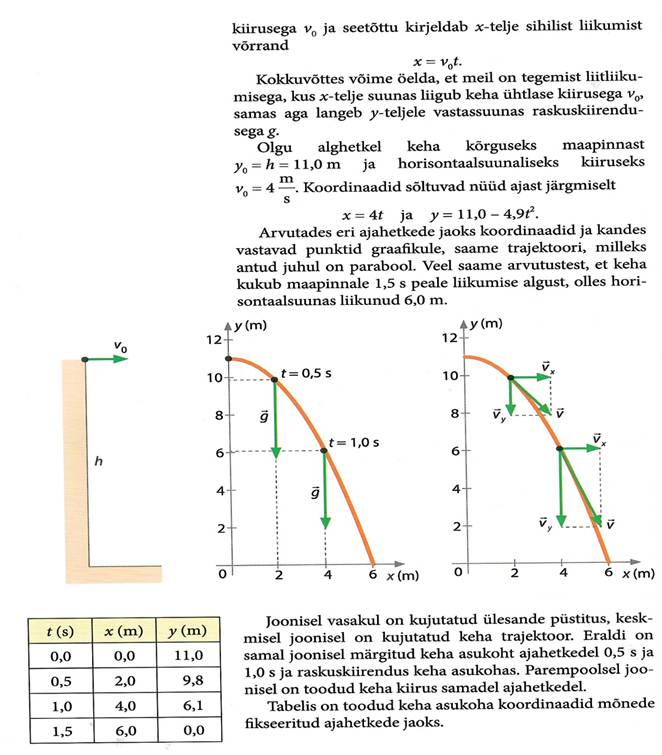
Ühtlaselt kiirenev liikumine

Enamasti ei liigu kehad ühtlaselt, mis tähendab, et kehade kiirus liikumisel muutub. Auto kiirus liikumahakkamisel kasvab aga pidurdamisel kahaneb. Vaatleme erijuhtu, ühtlaselt kiirenev liikumine. Nüüd liikumise kiirus muutub võrdeliselt ajaga:

v=at,

Siin konstantset suurust a nimetatakse  liikumise kiirenduseks. Kui alghetkel t=0 s on keha paigal, siis kiirendus a näitab mistahes võrdsetes ajavahemikes kasvab kkrus võrdse suuruse võrra, siit järeldub, et

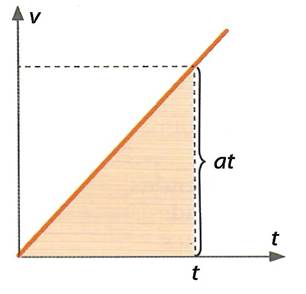
Kiirendus iseloomustab kiiruse muutumist ajaühikus.

Kui kiiruse ühikuks on  siis kiirenduse ühikuks on ehk meeter sekundis jagatud sekundiga.

Kui kiirendus on  siis suureneb kiirus igas sekundis   võrra ja liikumise algusest (paigalseisust) on kümne sekundi pärast kiiruseks:

v= 2x10=20 m/s

Läbitud teepikkuse arvutamne

Kuna teepikkus on võrdne arvuliselt võrdne kiiruse graafiku alla jääva pindalaga, siis siis on see võrdne ka joonisel toodud kolmnurga pindalaga (alus korda kõrgus jagatud kahega).

Teepikkuse sõltuvust ajast  kujutab graafikul olev parabool. Ühtlaselt kiireneval liikumisel kasvab teepikkus võrdeliselt aja ruuduga.

Liikumisel paigalolekust jääva kiirendusega a avalduvad kiirus ja läbitud teepikkus valemitega

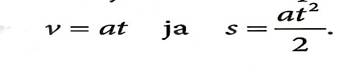
10L2

Keskmine kiirus

Hetkkiirus

10l1

LK 06.10

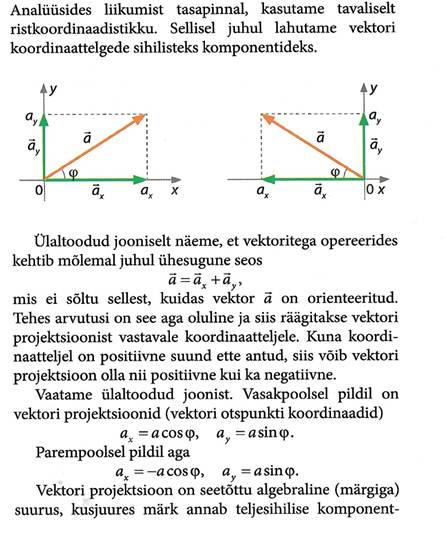
Skaalarid ja vektorid

Vektorite liitmine

Vektorite lahutamine

Vektori lahutamine komponentideks

Vektori projektsioon

10l2

10l1@stillen.ee

10LOODUS10

10l2@stillen.ee

10LOODUS20

10lk@stillen.ee

10KORVPALL

10h@stillen.ee

10HUMANITAAR

https://webmail.telia.ee/

aadress sisestada vastavalt tabelile ja siis ka parool vastavast tabelist

Ülesanne:

Kommentaariks lisame:

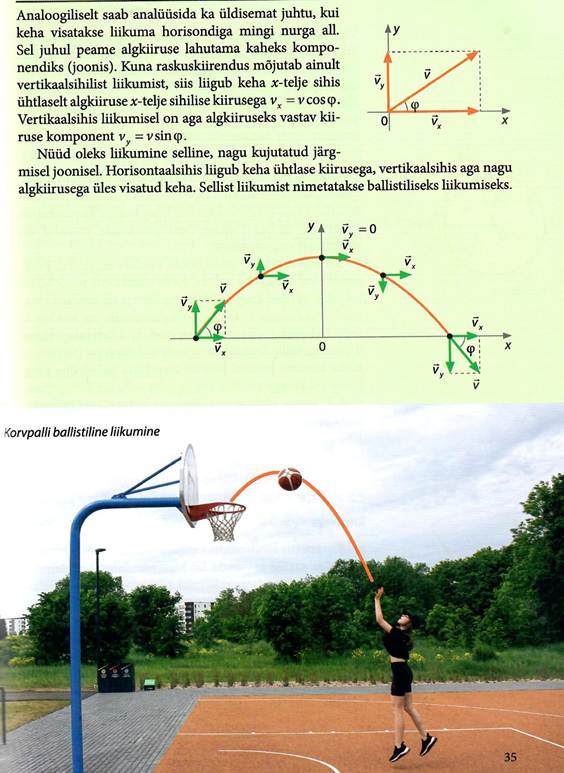
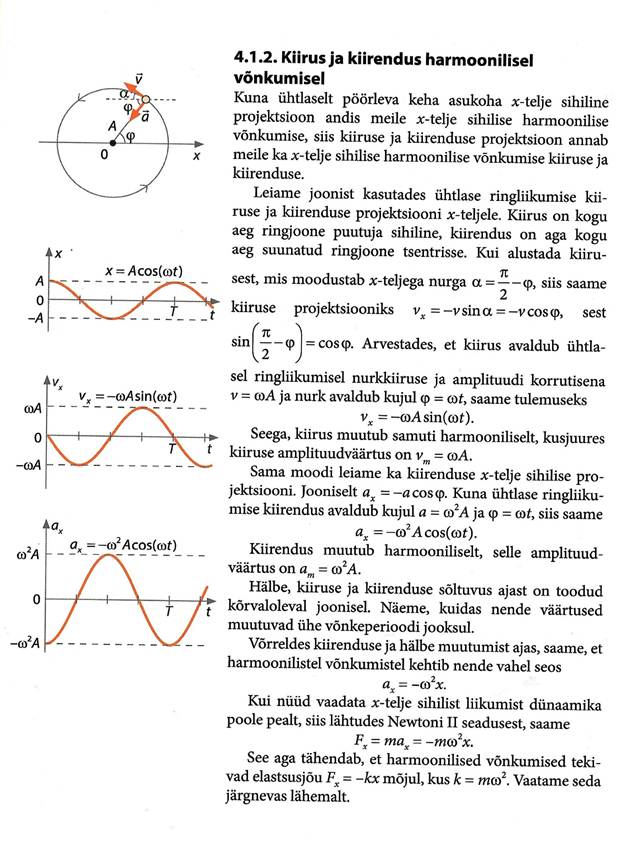
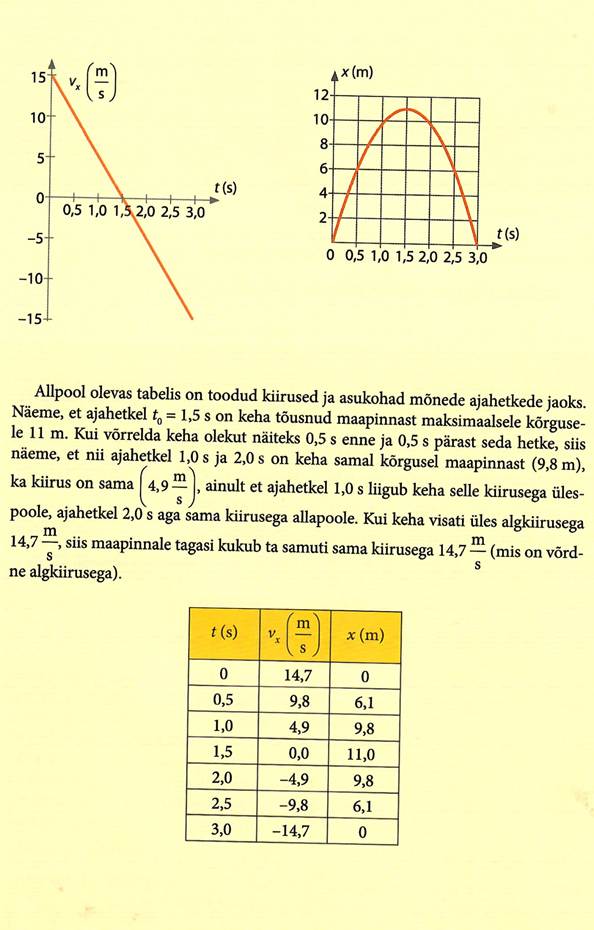
Ühtlane ringliikumine, joonkiirus ja nurkkiirus

Üks lihtsaimaid liikumisi tasandil on ühtlane ringliikumine. Siin on trajektooriks ringjoon. Mistahes võrdsetes ajavahemikes

läbitakse võrdsed teepikkused ehk võrdsed kaarepikkused. Kiiruse same jagades aja t jooksul läbitud teepikkuse s ajaga:

v=s/t.

Ühtlane ringliikumine on ka ühtlane tiirlemine. Näiteks lihtsustatult on ka Kuu tiirlemine ümber Maa, nagu ka planeetide

tiirlemine ümber päikese. Planeetide orbiidid on praktiliselt ju ringjoonelised.

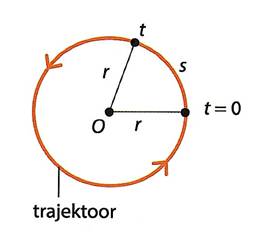
Ringliikumist on otstarbekas vaadelda ringjoone keskpunkti ja taustkeha suhtes.

Dünaamika

Ilma põhjuseta loodusnähtusi ei ole. Sama on ka kehade liikumisega. Ilma põhjuseta ei hakka ükski keha liikuma. Ega muuda oma liikumisolekut. Dünaamika ülesandeks on mehaanika osas näidata, mis põhjustab konkreetse keha liikumist. Dünaamika uurib mis põhjustab konkreetse keha liikumise tekkepõhjuse ja kuidas liikumine antud jõudude mõjul toimub.

Kehade vastastikmõju, jõud